Steps: 2177 Fuel Used: 1632 Total Cost: 3809
7.02user 0.11system 0:07.22elapsed 98%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (112major+30765minor)pagefaults 0swaps

This is Matthew Ogilvie's solution to the Mars Rescue Mission Challenge.
Downloads: The plain-C program can be downloaded by clicking here. This newer version fixes a slight bug in the remainingCost() function that occasionally caused the subsolution optimizer to find non-optimal subsolutions. You can also still get the older version. You can also download some additional tools I used (maps, scripts, and an alternate version of marsimg.cpp). Some sample solutions are listed below.
This implementation can find optimal solutions for moderately large maps (generally best with the --compress 1 option) fairly rapidly. Generally this mode is memory-usage bound.
It can also find good nonoptimal solutions for larger maps and/or multiple maps by optimizing subsequences of an initial rough solution that is found first. This tends to be CPU bound, with configurable tradeoffs between the memory/CPU usage, and the quality of the found solutions.
I learned about this contest from Slashdot. Some years ago my AI class attempted to solve a similar kind of problem (a "sliding numbers puzzle") using Lisp (it was a homework assignment), but due to limited memory in machines at the time, and the inherit inefficiencies of lisp, no one was not very successful at solving puzzles that had been more then slightly randomized. I remember thinking I could probably do much better with tight C code, but never got around to it. So when I saw a contest with actual prizes for coding up a similar type of algorithm, I overcame inertia and started coding. I haven't really kept track of how much time I've spent on this, but I'm sure it is more then I originally intended to.
The core "optimize()" algorithm just does a breadth-first search for the best path. It stores all "needs to be visited" states in a priority queue/heap.
It also stores all previously seen states. They are stored in either a hash table, or a tightly packed array attached to each square in the map. Overall the tightly packed array may have a slight advantage in memory usage over the heap when most states need to be seen (depending on how many states are unreachable but listed in the table), but where it really shines is when the total table size gets bigger then RAM. The packed array has better memory access locality, and when the table size is larger then RAM, continued progress is much faster then with the hash table.
Note that the hash table is still used as part of the heap when the packed array is enabled; in that case the hash table will only store the states that are also in the heap.
In order to handle bigger maps and/or multiple targets, it can also be put into a "rough solution followed by optimization" mode. The rough solution algorithm basically solves a version of the problem at the scale of the input map where the only legal moves are up, down, left, and right, with no concept of velocity. It then converts that rough solution to an unoptimized solution by running optimize() between each pair of adjacent states in the rough solution, and concatenating the result together. It then improves the unoptimized solution by splitting off short subsolutions, finding the start and end states of the subsolution, and using optimize() to find the best way to get from the start to end states of the subsolution.
Multitarget maps are solved by first constructing a cost table between all pairs of targets (finding improved rough paths as described above), then running a simulated annealing based traveling salesman algorithm on the cost table. It then composes a full solution from the found target sequence, and uses the "improve" algorithm to improve it further.
The optimize() routine also has a "remainingCost()" heuristic that does a conservative estimate (never over-estimate) of the remaining cost to reach the end state. This is only enabled when doing subsolution optimizations, since it won't work very well if there are a lot of of twists and turns before reaching the end state.
With a small subsolution size (12 to 15), I can get a reasonable solution to map.txt in about an hour without swapping on a puny 200MHz PPro with only 64 MB ram.
Most of my real runs were done on a 2.6GHz P4 with 1GB ram. It can find optimal solutions to map.txt in 4 to 6 minutes (using the compressed state mode), and digs slightly into swap space. I did not try to do optimal solutions of any of the bigger maps.
Could easily force a particular path by inserting extra walls in the map.
Could easily avoid hitting walls by giving a large --wall cost.
A bit harder to ensure soft landing at end: need to modify termination conditions in the code with with more special cases.
To extend to 3D: Rule extensions: Add 2 more thrusters, controlled with one bit each. New direction breaks into 10 subpositions per map position, and has 21 different velocities (-10<=vz<=10).
Rough solution is probably easy. Improving rough solution might be difficult; you might be stuck only being able to improve very short subsolutions. Optimal solution for anything larger then very very small is hard.
Theoretically it could be extended to find optimal solutions to multitarget maps by using a bitmask of acquired targets, instead of a target sequence number. But it is likely it would need good hueristics (better then remainingCost()) to solve very many targets and/or anything very large at all.
Slightly increase caching state information to improve rough solution improvement performance?
Remember the optimal path between adjacent rough states, in case that transition is needed for other targets.
Remember optimal paths for specific subsolutions when improving a solution, so that as it repeats itself, if it tries that same subsolution again, it doesn't have to recalculate an already-optimal path. It could get most of the bang just remembering the paths for the previous and current "repeat" iterations.
Maybe there are other small caches that might significantly improve performance for minimal memory usage?
During "improvement", perhaps allow targeting a sequence of end states from the input sequence, for a wider objective cross section?
Maybe eliminate "all seen state" table; only remember "need to be processed"? I'm worried this would cause a lot of duplicated effort (re-calc a state multiple times). But maybe an intermediate solution would be possible: continue to have a table bigger then the heap, but allow stuff to expire from and be taken out of the table eventually.
Or maybe keep some kind of "coarse" (map-resolution?) cache; ignore new state if it is substantially worse then the best in its coarse collection of states.
Research would be needed to decide how either of these might be done.
Perhaps use an etching/line-thinning algorithm to convert traversable areas to a single pixel thick, convert to a logical graph structure, and use some variations of the "rough" solution idea to drive solution finding.
Go even more coarse then map resolution, in some kind of divide-and-conquer algorithm?
A totally different optimization approach: Use genetic algorithm technique to improve initial rough solution?
Could eliminate "cost" from CompressedState completely (recompute from action and remainingCost() whenever needed...). But this weaken cache locality.
Could eliminate 1 or 2 bits per velocity with smarter implementation. Could eliminate "action", it can be reconstructed by finding the "optimal" way to get to this state from previous one...
Three bytes per state should be possible (manual bit mangling to avoid structure alignment of 4). Two bytes per state might even be possible with some effort.
UPDATE (31 Jan) now fixed: Possible bug: On some maps with some configurations, some consistency-checking code is occasionally detecting a situation when an "improved" solution ends up worse (with a higher cost). I'm a bit confused: Although there might be some problem with the remainingCost() heuristic, any cost increase should be detected and avoided at the subsolution level before it gets to the overall solution. Maybe I'll have time to track this down before the end of the contest.
Weaknesses of subsolution optimization strategy:
When configured to do a rough solution optimized for cost on a large map, it often finds a solution that uses more fuel then what it finds when it is optimizes for steps. Probably because for short subsolutions, step optimization can "waste" fuel to get up to speed in the middle, and then later iterations can get the ends up to speed as well. But for fuel, the subsolution optimization avoids the fuel to get up to speed, to the detriment of the overall solution...
Perhaps adjust the balance of the step and wall costs?
Perhaps adjust the algorithm to use different cost functions early in optimization vs late in optimization?
The obvious way to resolve this is to increase the size of subsolutions that it optimizes.
Possibly set up a system where optimizer sets up and uses moderately sized target "cross sections" before exactly matching up with final end point of subsolution? The objective would be to increase the subsolution size attempted at a time, without increasing memory or CPU requirements.
Perhaps some higher level caching scheme could improve it. (see discussion above).
Run on a 2.6 GHz P4 with 1GB ram. The optimal solutions for map.txt had approximately 1GB memory footprint. The memory usage for "improved rough" runs increase and decrease a lot during a run, but seemed to max out at about 300MB at times.
Except where otherwise noted, all solutions were generated using the 24 Jan version of the program.
Steps: 2177 Fuel Used: 1632 Total Cost: 3809
7.02user 0.11system 0:07.22elapsed 98%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (112major+30765minor)pagefaults 0swaps

Steps: 282 Fuel Used: 169 Total Cost: 28369
303.87user 1.59system 5:10.88elapsed 98%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (503major+222350minor)pagefaults 0swaps

Steps: 318 Fuel Used: 146 Total Cost: 14918
342.50user 1.72system 5:47.23elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (705major+244066minor)pagefaults 0swaps

Steps: 283 Fuel Used: 169 Total Cost: 28469
275.28user 1.84system 4:37.53elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (164major+213405minor)pagefaults 0swaps

Steps: 289 Fuel Used: 161 Total Cost: 16389
249.17user 1.71system 4:14.55elapsed 98%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (389major+226234minor)pagefaults 0swaps

Steps: 286 Fuel Used: 172 Total Cost: 28772
2461.26user 28.30system 41:34.04elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (163major+4041295minor)pagefaults 0swaps

Steps: 292 Fuel Used: 164 Total Cost: 456
4657.34user 54.24system 1:18:41elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (113major+7678833minor)pagefaults 0swaps

Steps: 291 Fuel Used: 160 Total Cost: 451
6448.97user 70.29system 1:49:15elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (212major+10198086minor)pagefaults 0swaps

Steps: 662 Fuel Used: 352 Total Cost: 66552
4953.58user 61.36system 1:23:46elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (139major+8662709minor)pagefaults 0swaps

Steps: 678 Fuel Used: 316 Total Cost: 994
2692.73user 38.46system 45:38.24elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (113major+5813412minor)pagefaults 0swaps

Steps: 1694 Fuel Used: 974 Total Cost: 170374
56930.05user 865.00system 16:24:39elapsed 25%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (186major+152172232minor)pagefaults 0swaps

Steps: 1744 Fuel Used: 842 Total Cost: 2586
124366.48user 1683.65system 35:41:28elapsed 31%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (61817major+281477630minor)pagefaults 0swaps

Steps: 1755 Fuel Used: 879 Total Cost: 2634
56894.57user 877.77system 18:38:39elapsed 22%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (14543major+150292210minor)pagefaults 0swaps

Steps: 278 Fuel Used: 218 Total Cost: 28018
1431.91user 17.95system 42:24.85elapsed 56%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (600major+2356738minor)pagefaults 0swaps
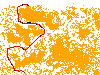
Steps: 302 Fuel Used: 176 Total Cost: 478
1280.52user 16.91system 22:09.51elapsed 97%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (113major+2381925minor)pagefaults 0swaps
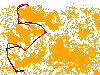
Steps: 726 Fuel Used: 652 Total Cost: 73252
16553.34user 233.34system 4:42:55elapsed 98%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (127major+37793057minor)pagefaults 0swaps
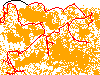
Steps: 812 Fuel Used: 545 Total Cost: 1357
15542.79user 236.77system 4:25:51elapsed 98%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (187major+38554585minor)pagefaults 0swaps
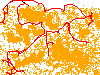
Steps: 13 Fuel Used: 12 Total Cost: 1312
6.57user 0.11system 0:06.71elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (113major+10566minor)pagefaults 0swaps

Steps: 516 Fuel Used: 318 Total Cost: 51918
112.43user 2.58system 1:55.65elapsed 99%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (113major+494584minor)pagefaults 0swaps

Steps: 13 Fuel Used: 12 Total Cost: 25
6.60user 0.06system 0:06.73elapsed 98%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (113major+11064minor)pagefaults 0swaps

Steps: 601 Fuel Used: 327 Total Cost: 928
93.57user 2.06system 1:36.60elapsed 98%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (113major+476188minor)pagefaults 0swaps

Steps: 301 Fuel Used: 189 Total Cost: 30289
2572.18user 42.48system 45:58.88elapsed 94%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (0major+0minor)pagefaults 0swaps

Steps: 315 Fuel Used: 172 Total Cost: 487
4112.07user 74.66system 1:13:27elapsed 94%CPU (0avgtext+0avgdata 0maxresident)k 0inputs+0outputs (0major+0minor)pagefaults 0swaps
